7 LAB IX: Correlation

When we have finished this Lab, we should be able to:

Learning objectives

Understand the concept of correlation of two numeric variables.
Compute Pearson’s r (or Spearmans $r_{s}$ ) correlation coefficient between two numeric variables
Discuss the possible meaning of correlation that we observe.

In this Lab, we will use the data from “LungCapacity” dataset.(Note: This starts by assuming we know how to get data into Jamovi).

7.0.1 Opening the file

Open the dataset named “LungCapacity” from the file tab in the menu:

The dataset “LungCapacity” has 725 participants and includes two variables. The numeric variables of interest are the Age and the LungCap (Figure 8.1). Double-click on the variable name Age and change the measure type from nominal to continuous .

7.0.2 Research question

Let’s say that we want to explore the association between age (in years) and lung capacity (in liters) for the sample of 725 participants in a survey.

7.0.3 Hypothesis Testsing

Null hypothesis and alternative hypothesis

$H_{0} :$ there is not association between age and lung capacity ( $ρ = 0$ ).
$H_{1} :$ there is association between age and lung capacity ( $ρ \neq 0$ ).

7.0.4 Graphical display with a scatter plot

A first step that is usually useful in studying the association between two continuous variables is to prepare a scatterplot of the data. The pattern made by the points plotted on the scatterplot usually suggests the basic nature and strength of the association between two variables.

On the Jamovi top menu navigate to

as shown below in Figure 7.2.

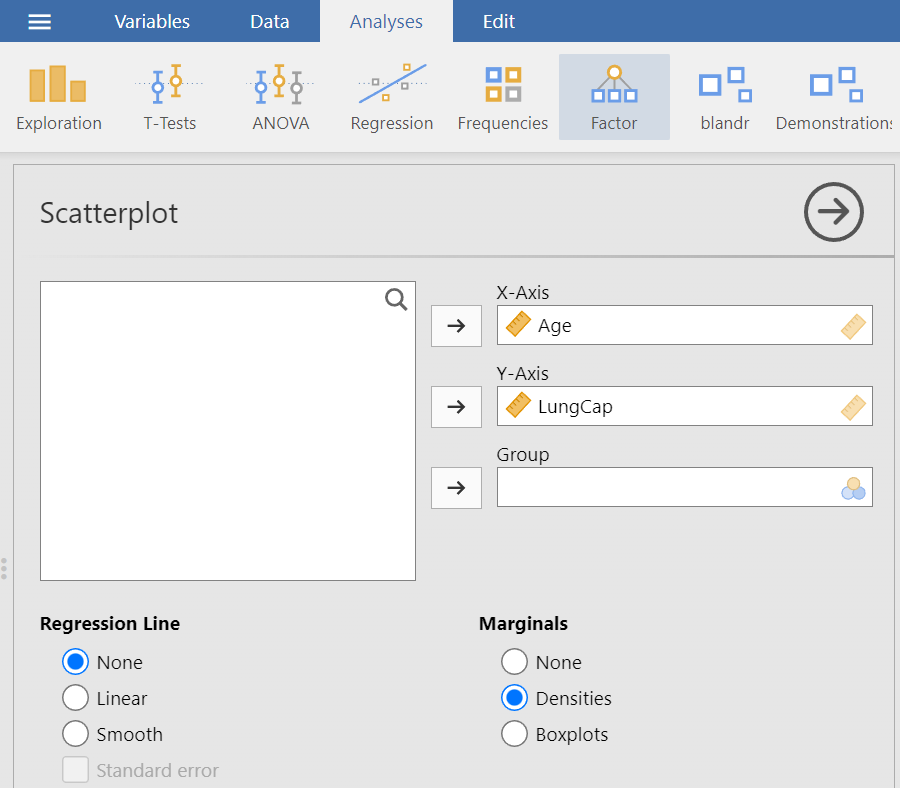
Figure 7.2: In the menu at the top, choose Analyses > Exploration > Scatterplot.

The Scatterplot dialogue box opens (Figure 7.3). Transfer the Age and LungCap variables from the left-hand pane into the X-Axis and Y-Axis fields on the right-hand side, respectively, by highlighting the variables and pressing the Arrow Button (). Alternatively, drag and drop the variables. Finally, from Marginals click on the “Densities” radio button. We will end up with the following screen:

Figure 7.3: The Scatterplot dialogue box options.

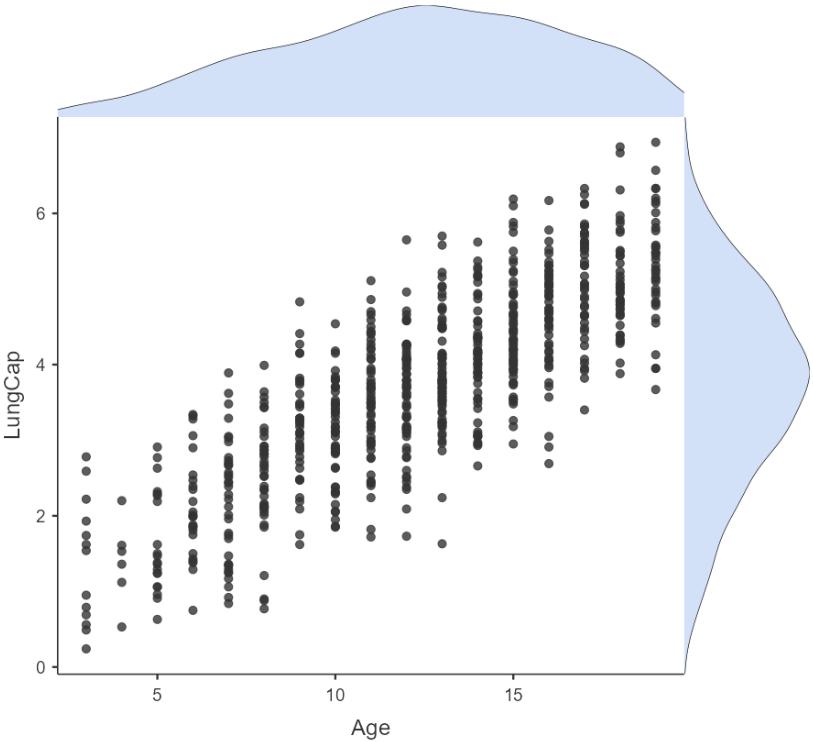
The resulting graph looks like this (Figure 7.4):

Figure 7.4: The Scatter of Age and Lung Capacity with the marginal density plots

The above density plots (light blue histograms) show that the data are approximately normally distributed for both Age and LungCap (we have a large sample so the graphs are reliable).

Additionally, the points in the scatter plot seem to be scattered around an invisible line. The scatter plot also shows that, in general, older participants tend to have higher lung capacity (positive association).

The Pearson’s correlation coefficient can quantify the strength of this linear association (alternative is Spearman’s correlation coefficients).

7.0.5 Applying the Pearson’s correlation coefficient, r

Running correlation in Jamovi requires only a few steps once the data is ready to go. In the top menu navigate to:

as shown below in Figure 7.5.

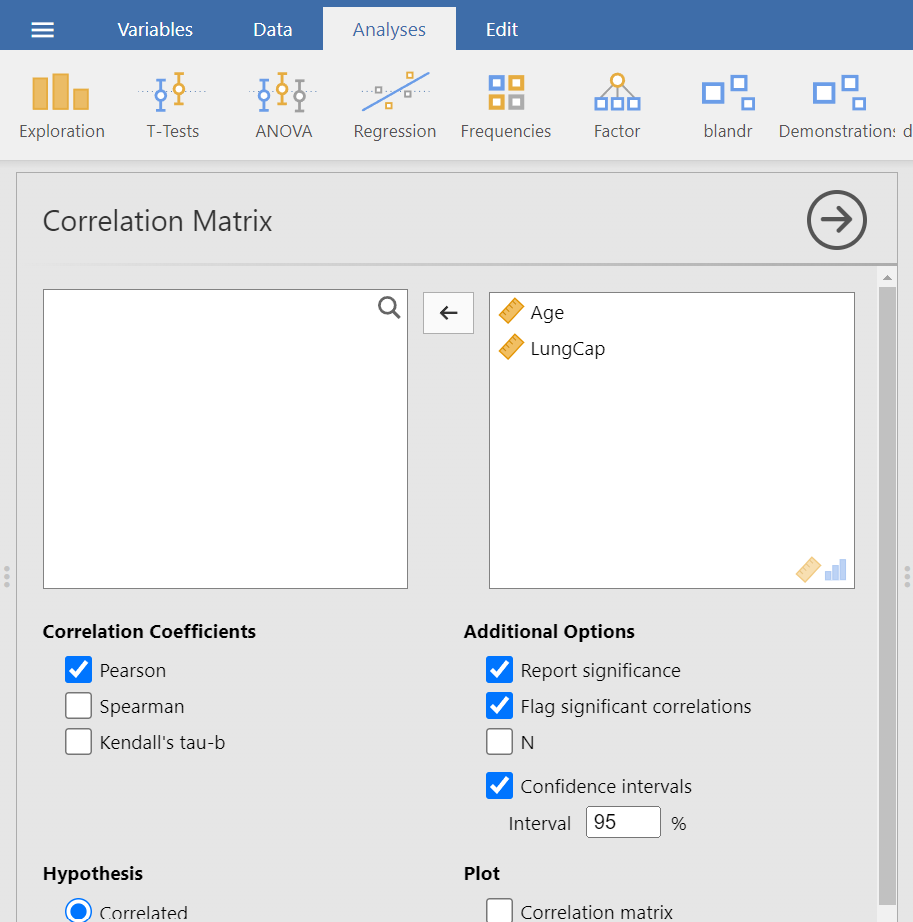
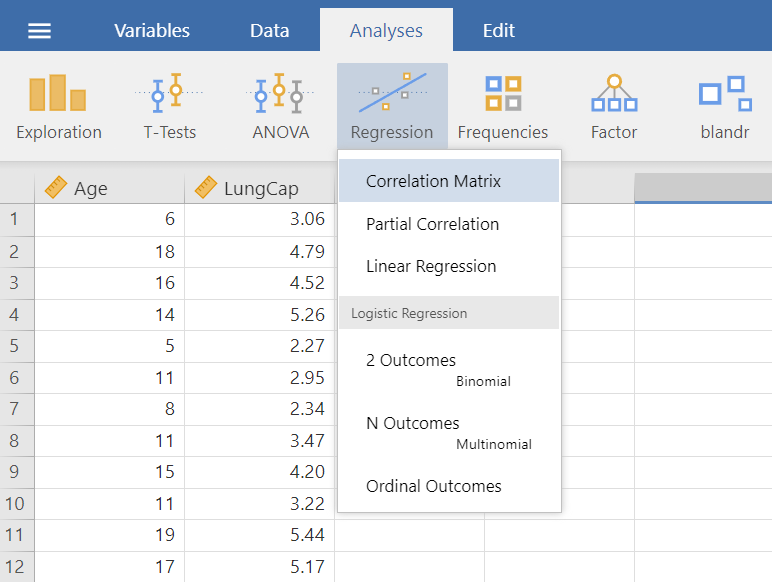
Figure 7.5: In the menu at the top, choose Analyses > Regression > Correlation Matrix.

The Correlation Matrix dialogue box opens (Figure 7.6). Transfer both Age and LungCap variables from the left-hand pane into the right-hand pane by highlighting the variables and pressing the Arrow Button (). Additionally, from the Correlation Coefficients choices we can select between the following three options: Pearson’s, Spearman, or Kendall’s coefficient. We keep the default choice of “Pearson”. Finally, from Additional Options check “Flag significant correlations” and the “Confidence Intervals” boxes. We will end up with the following screen:

Figure 7.6: The Correlation Matrix dialogue box options. Drag and drop the **Age** and **LungCap** into the right-hand pane. Check the boxes of interest in the additional options.

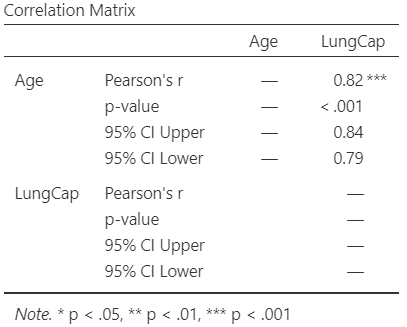
The output table should look like the following (Figure 7.7):

Figure 7.7: The correlation matrix table.

Interpretation of the results

There is evidence of a very strong, positive, linear association between Age and Lung Capacity (r= 0.82, 95% CI: 0.79 to 0.84, p < 0.001) which is significant.