4 LAB IV: Sampling distribution and Confidence Interval

When we have finished this Lab, we should be able to:

Learning objectives

Know the basic properties of sampling distribution of mean
Understand the Central Limit Theorem (CLM)
Understand the concept of the confidence interval of mean

4.1 The Sampling Distribution of mean and the CLT

In this Lab we will learn the Central Limit Theorem (CLT), which is the basis for many statistical concepts. We are going to explore this concept with the help of a Shiny application. So, clink on the following link CLM.

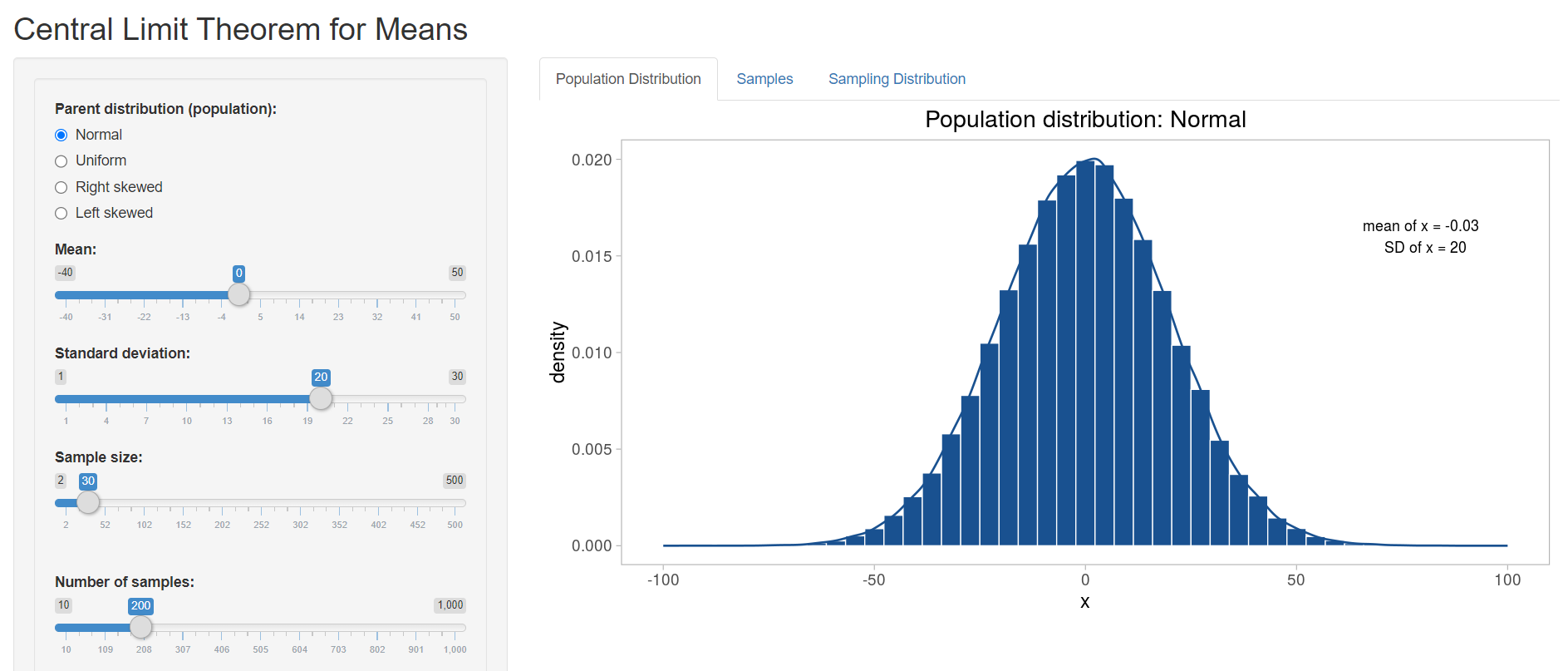
A Shiny app opens in a web window as shown below (Figure 4.1):

Figure 4.1: The Shiny application simulating the Central limit Theorem for Means

To the left is the interactive panel with radio buttons and slider bars, and to the right there are three tabs:

Population Distribution.
Samples.
Sampling Distribution.

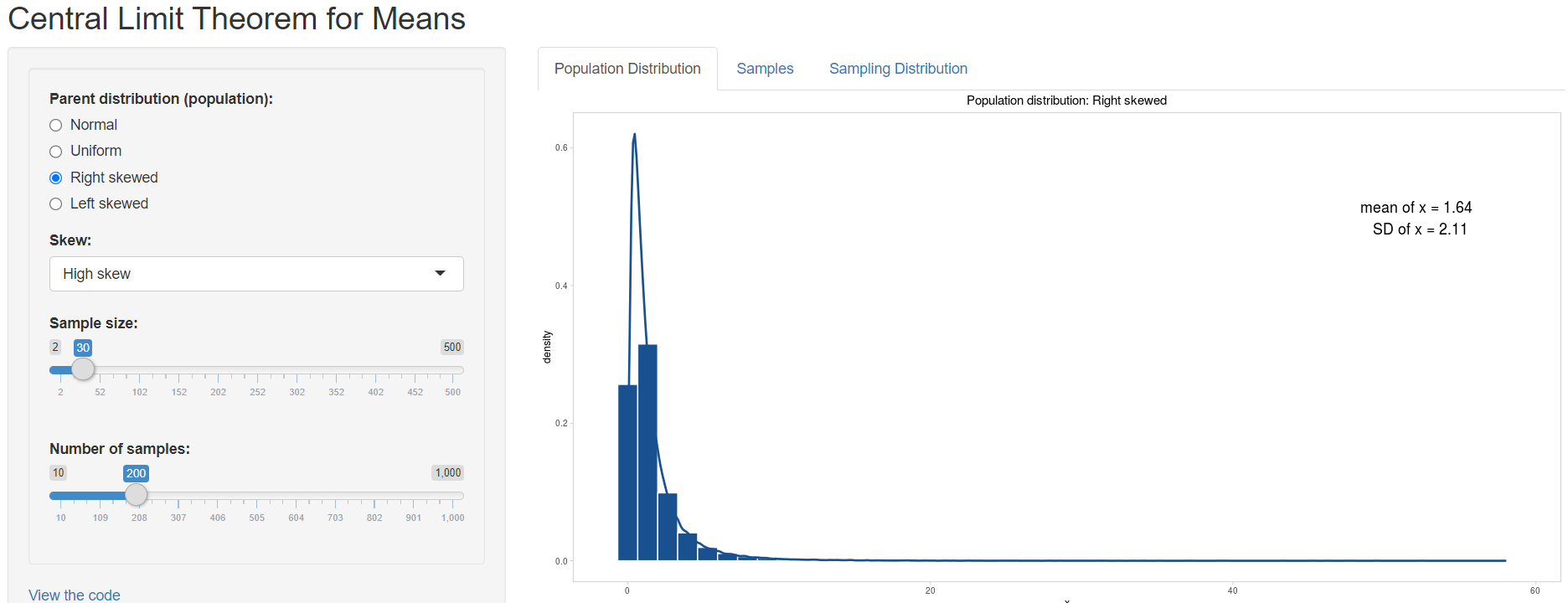
First we are asked to choose from a Normal, Uniform, Right Skewed or Left Skewed Parent distribution (Population) from the left panel. Let’s select Right skewed and then High skew from the drop down menu with the name Skew, as shown in Figure 4.2.

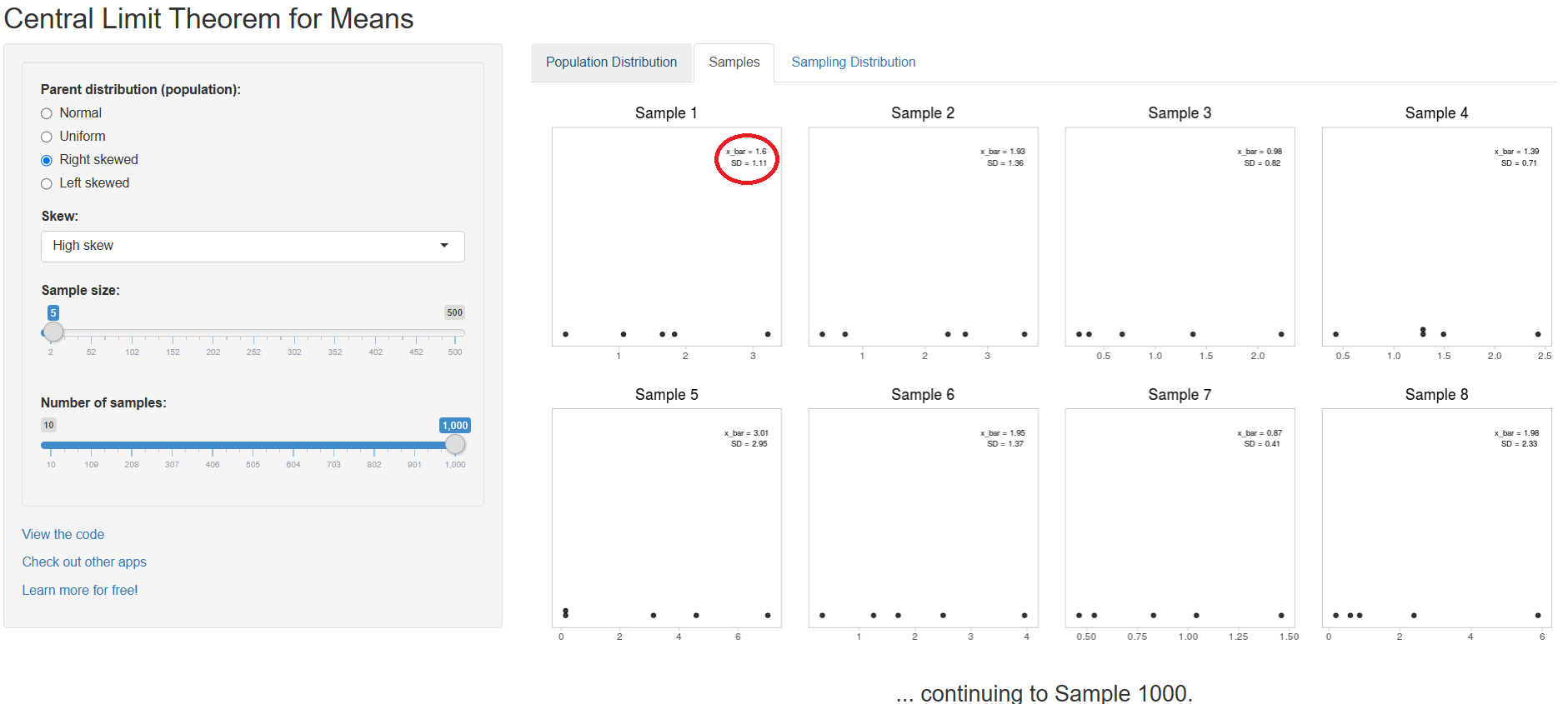
Figure 4.2: The case of a high right skewed population distribution

Next we set the Sample size slider bar to 5 and the Number of samples to 1000, then select the Samples tab, as shown in Figure 4.3. The first eight samples randomly drawn from the original distribution are demonstrated in the panel. For example, in the first box labeled Sample 1, we observe five data points (the sample size we set), along with their sample mean and standard deviation (highlighted in the red circle).

Figure 4.3: First eight samples randomly drawn from the original distribution.

Finally, we select the Sampling distribution tab, which displays the distribution of the 1000 sample means. We observe that this distribution is right skewed with mean approximately equal to population mean (Figure 4.4).

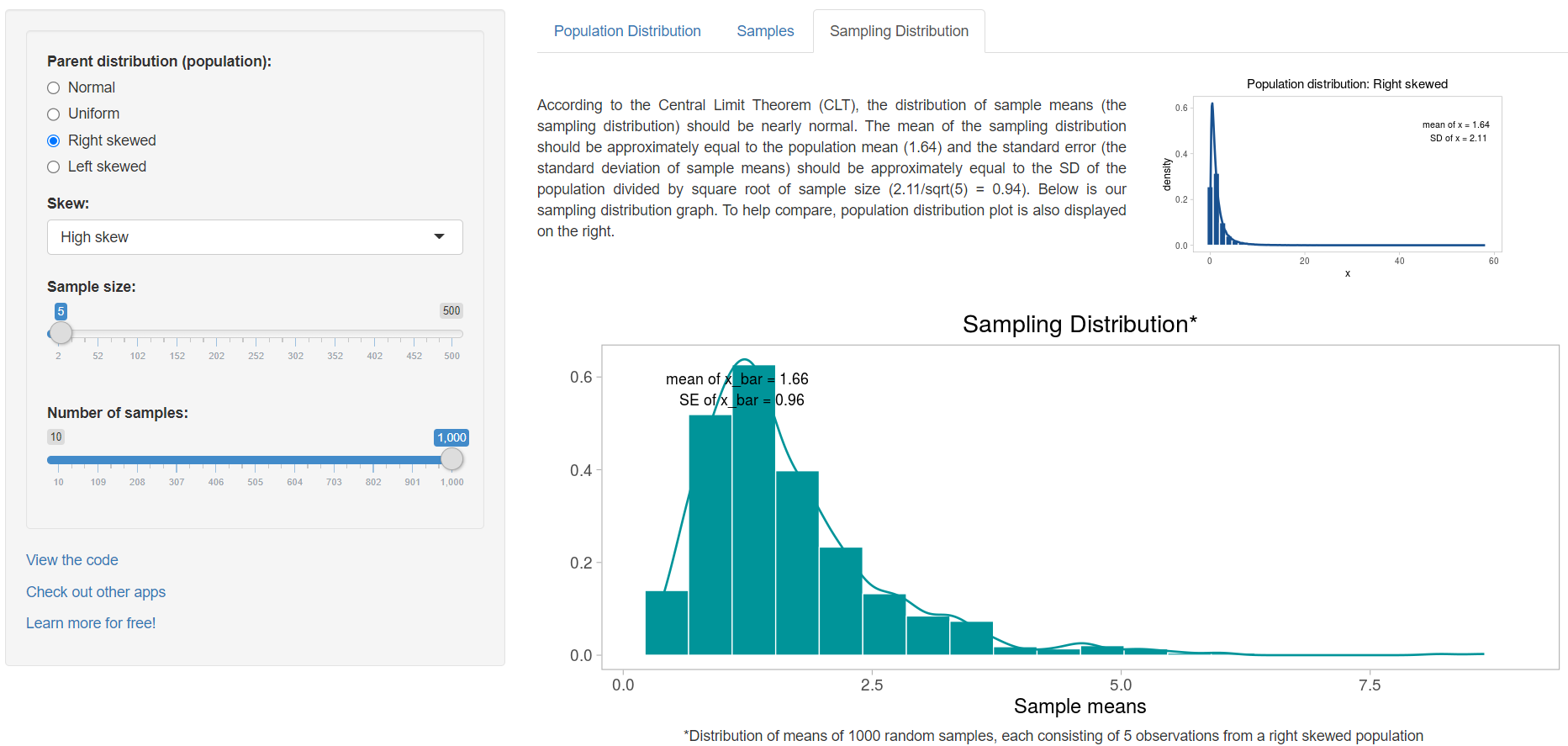
Figure 4.4: Distribution of means of 1000 random samples, each consisting of 5 observations from a high right skewed population distribution

Now, try to increase the sample size to 30 (Figure 4.5):

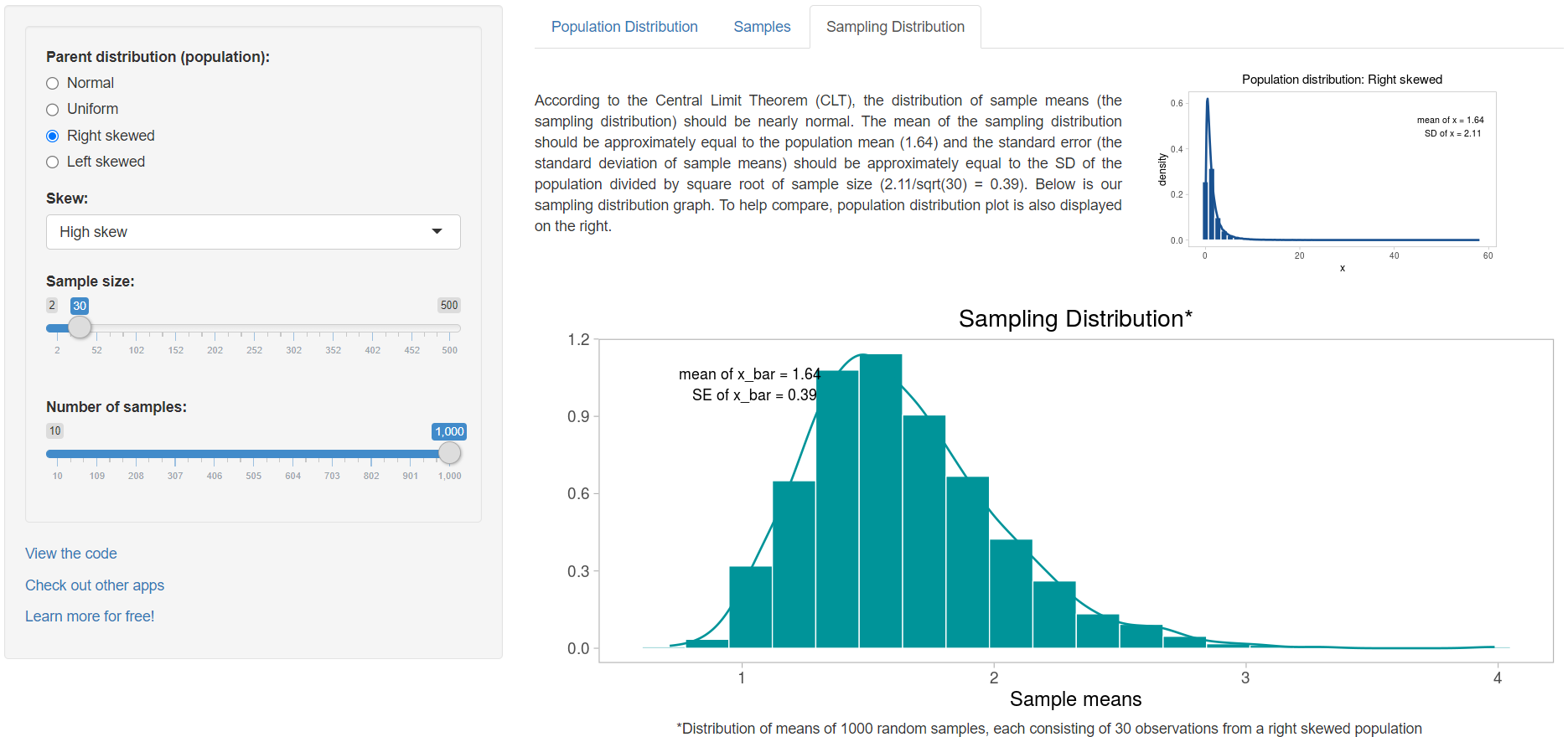
Figure 4.5: Distribution of means of 1000 random samples, each consisting of 30 observations from a high right skewed population distribution

and then increase it to 200 (Figure 4.6):

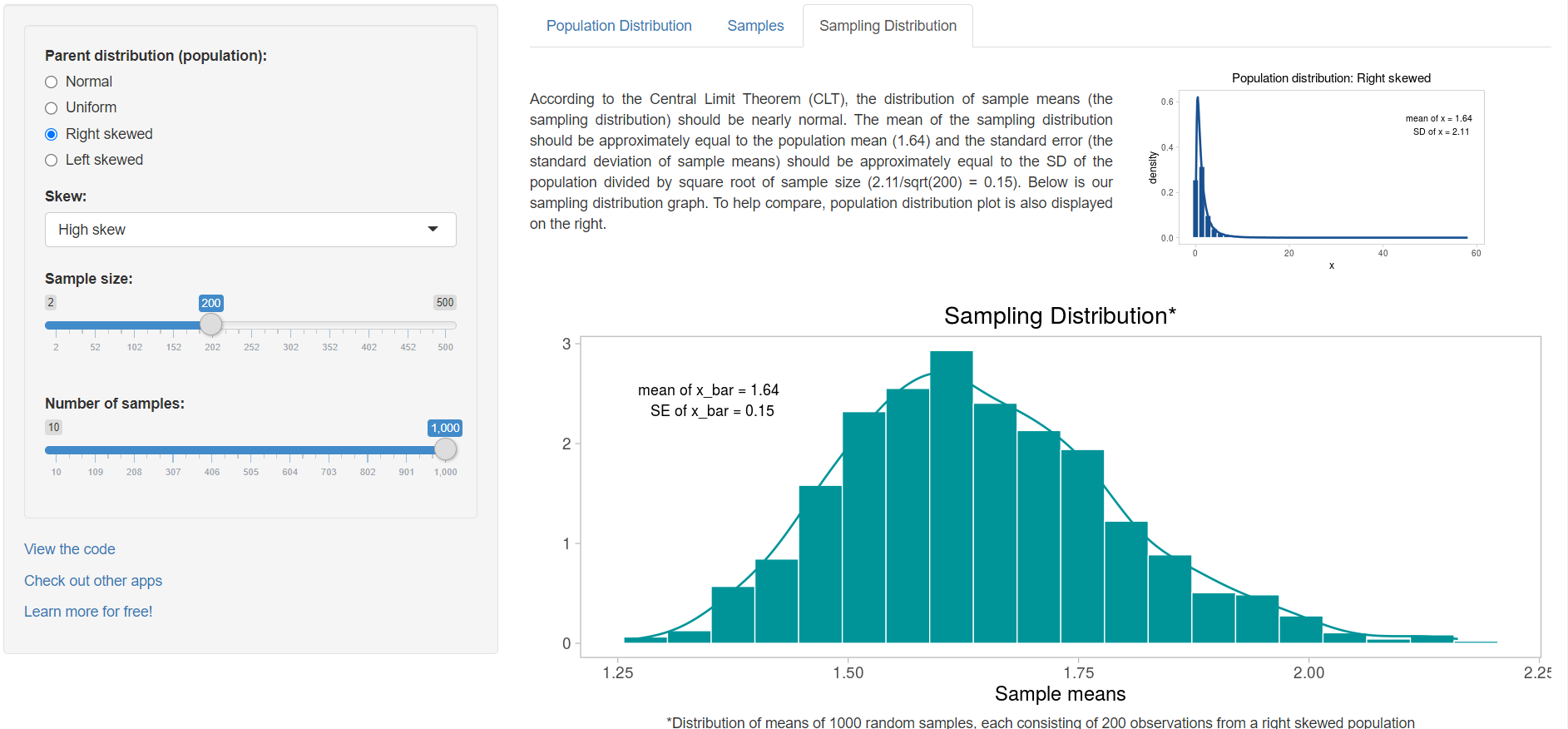
Figure 4.6: Distribution of means of 1000 random samples, each consisting of 200 observations from a high right skewed population distribution

We observe that the sampling distribution becomes closer and closer to Normal and the standard error of the mean, SE, (the standard deviation of sample means) gets smaller as the sample size increases. The important point is that whatever the parent distribution of a variable, the distribution of the sample means will be nearly Normal, as long as the samples are large enough.

Properties of the sampling distribution of the mean

The mean of the sampling distribution is the same as the mean of the population.
The standard deviation of the sampling distribution (i.e., the standard error) gets smaller as the sample size increases.
According to the Central Limit Theorem (CLM), the shape of the sampling distribution becomes normal as the sample size increases regardless of the variable’s population distribution.

4.2 The confidence interval of mean

We are going to explore the concept of confidence interval (CI) of mean with the help of a Shiny application. So, clink on the following link CIs.

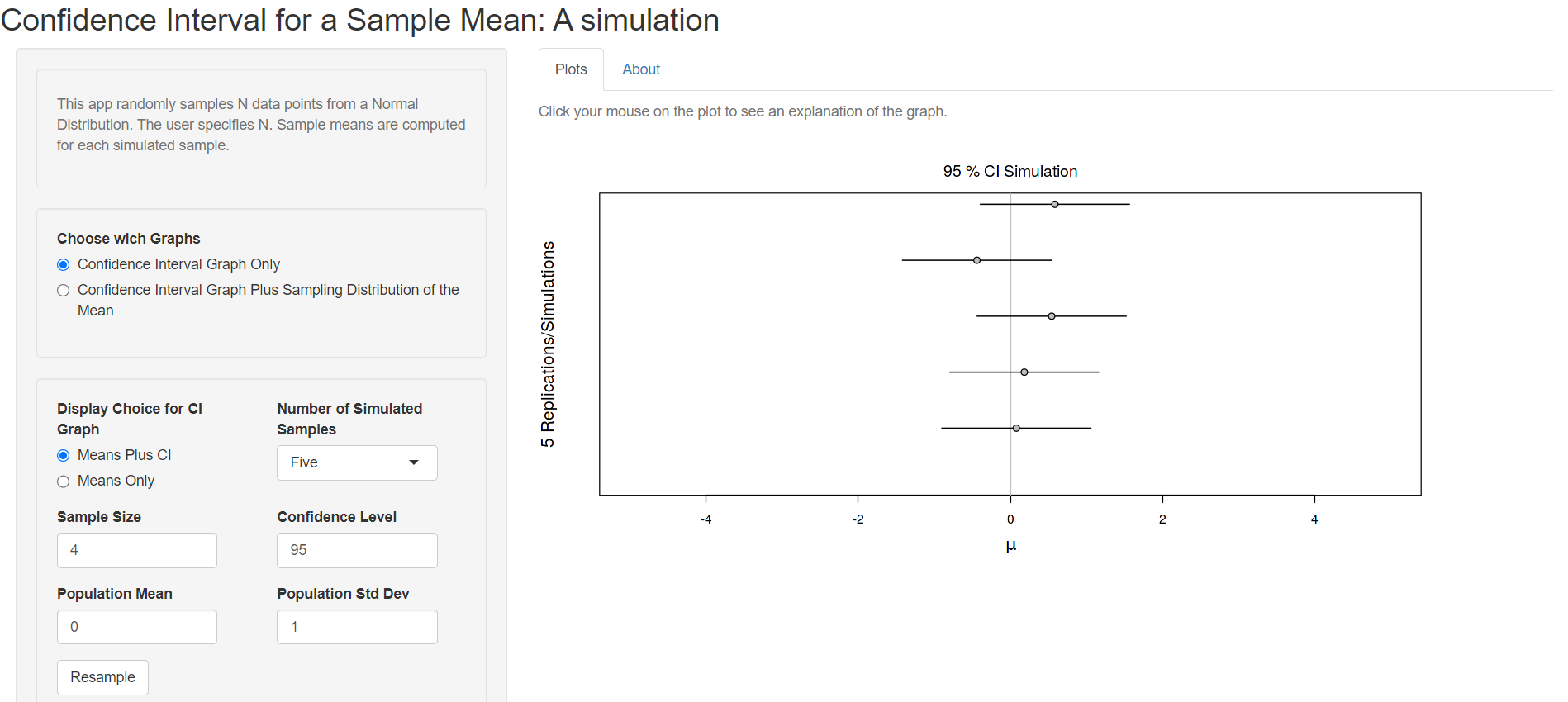
A Shiny app opens in a web window as shown below (Figure 4.7):

Figure 4.7: Shiny application that simulates the concept of confidence interval (CI) of mean

On the left is the interactive panel with radio buttons and drop down menus, and to the right there are two tabs:

Plots.
About.

We retain active the Plots tab.

First we are asked to choose if we want the Confidence Interval Graph only or the Confidence Interval Graph Plus Sampling Distribution of the Mean. Let’s select the first choice and set the Number of Simulated Samples to one and the Sample Size to 10 from the drop down menus, as shown in Figure 4.8. A horizontal bar will be created which represents the confidence interval (CI), centered on the sample mean (point). In this case, the 95% CI for the sample mean includes the true value of the population mean (it crosses the solid vertical line) and it is drawn as a black line.

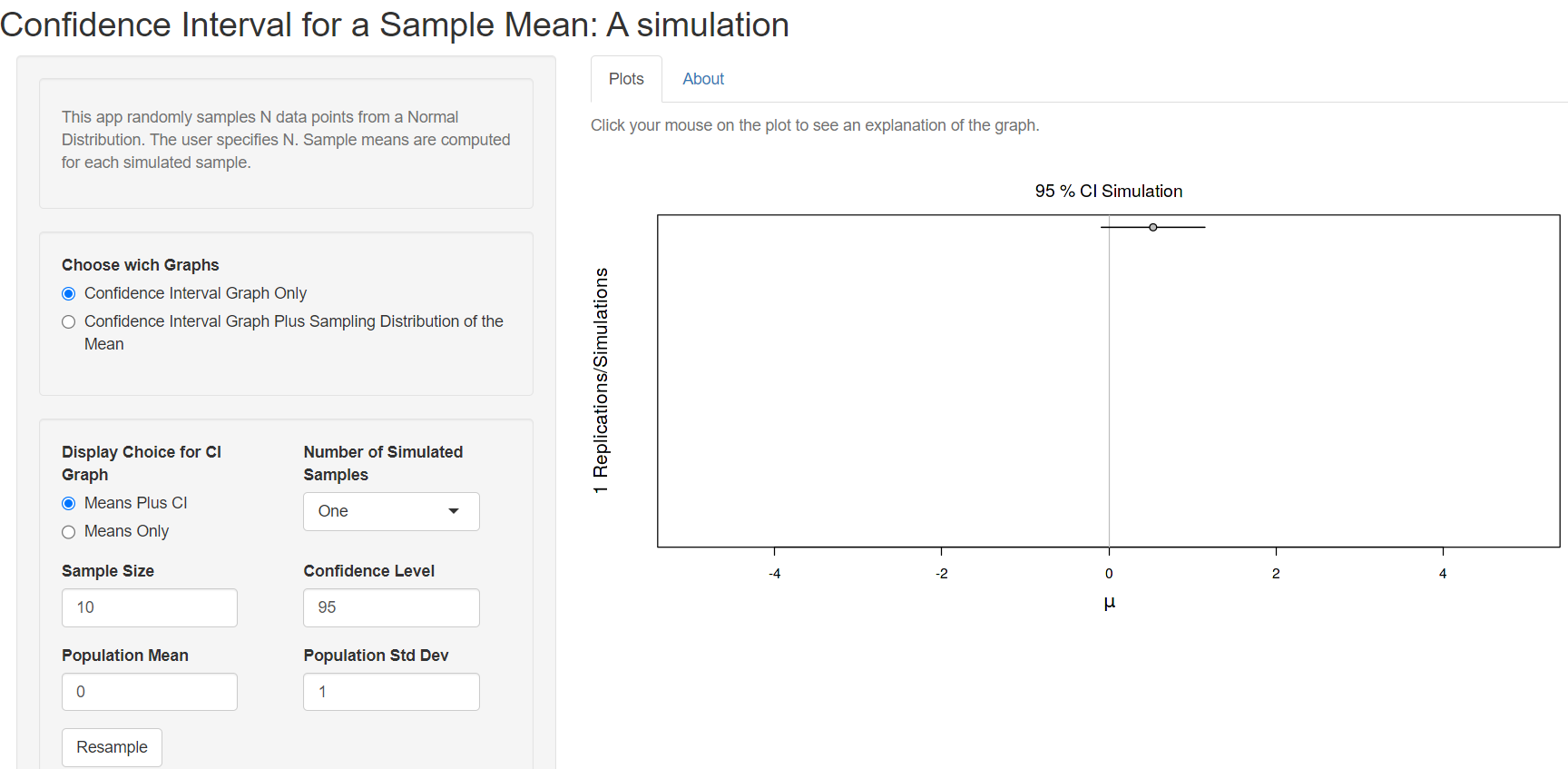
Figure 4.8: Confidence Interval Graph with one random sample of 10 observations selected from a normal population distribution

Now, try to increase the Number of Simulated Samples to 100 (Figure 4.9):

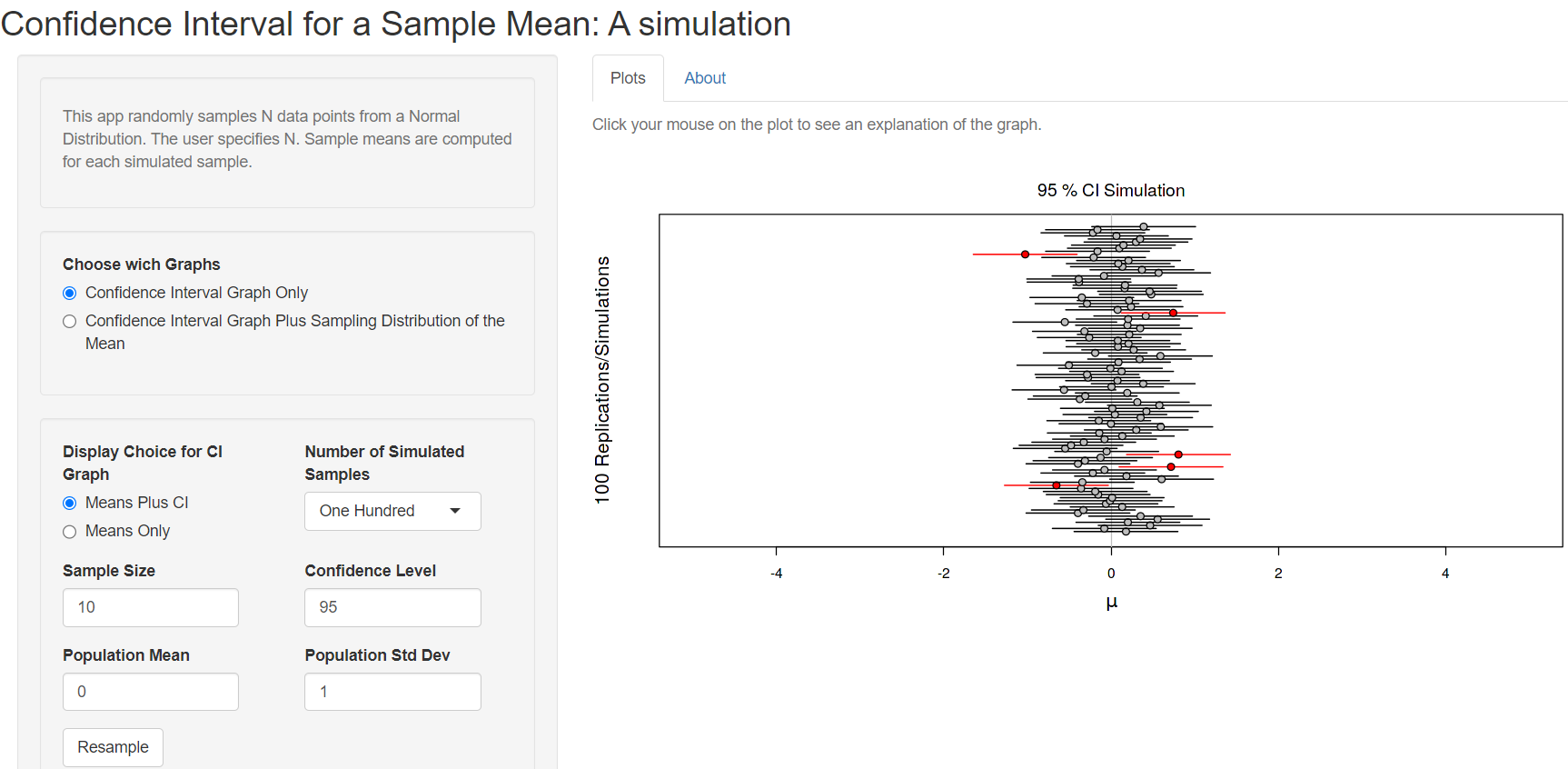
Figure 4.9: Confidence Interval Graph with 100 random samples, each consisting of 10 observations from a normal population distribution

We observe that 5 out of 100 confidence intervals (red horizontal lines) do not include the true population mean (the solid vertical line) (Figure 4.9). This is what we would expect – that the 95% confidence interval will not include the true population mean 5% of the time.

Next, we create the confidence intervals of 100 randomly generated samples of size = 50 from the population (Figure 4.10):

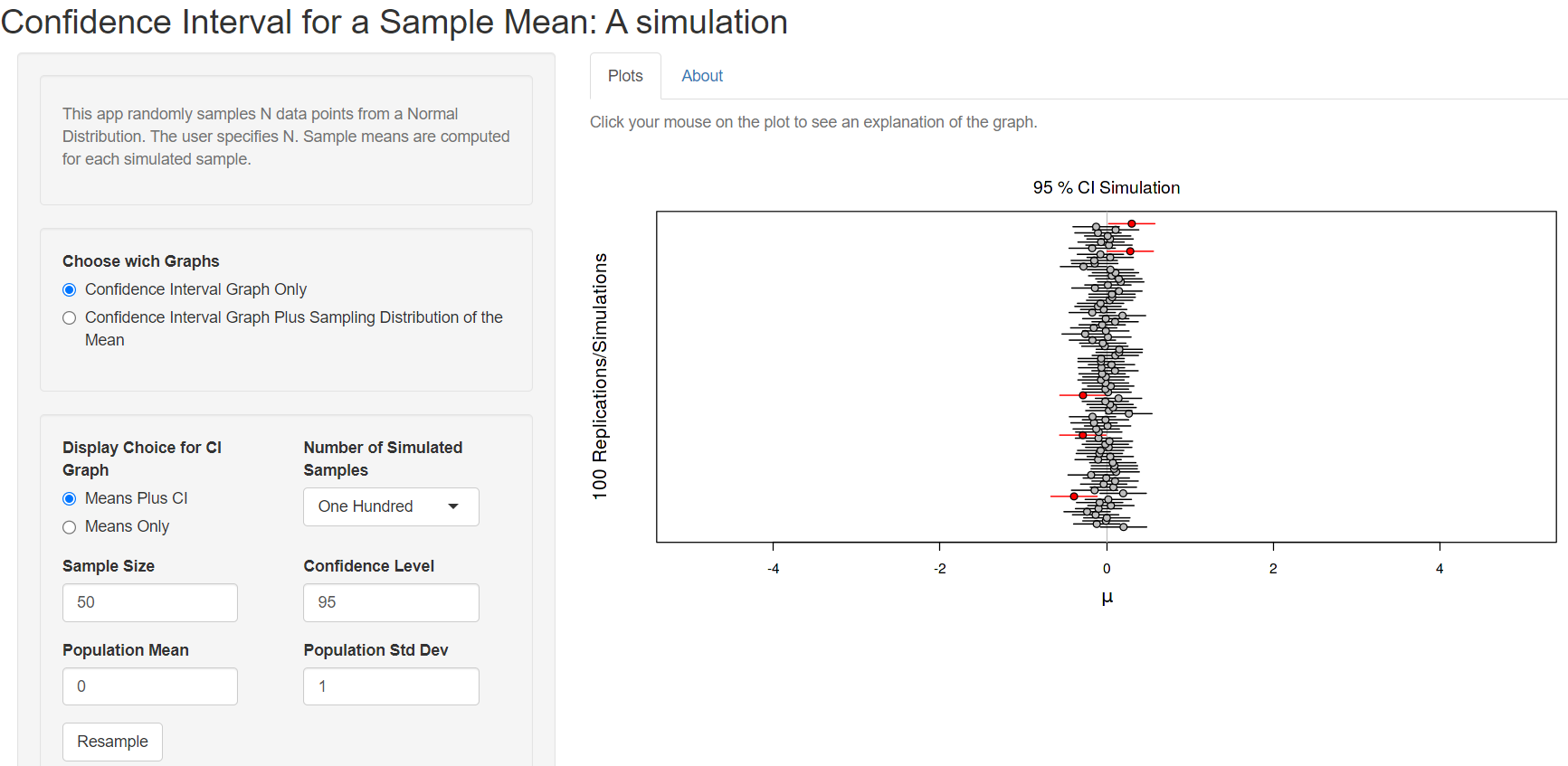
Figure 4.10: Confidence Interval Graph with 100 random samples, each consisting of 50 observations from a normal population distribution

We observe that the sample means are closer to the true population mean and the 95% CIs of the mean become narrower (Figure 4.10) increasing the sample size.