8 LAB X: Simple linear regression

When we have finished this Lab, we should be able to:

Learning objectives

Understand the linear regression model
Explore how a factor (independent variable) affect a response (dependent) variable.
Interpret the results

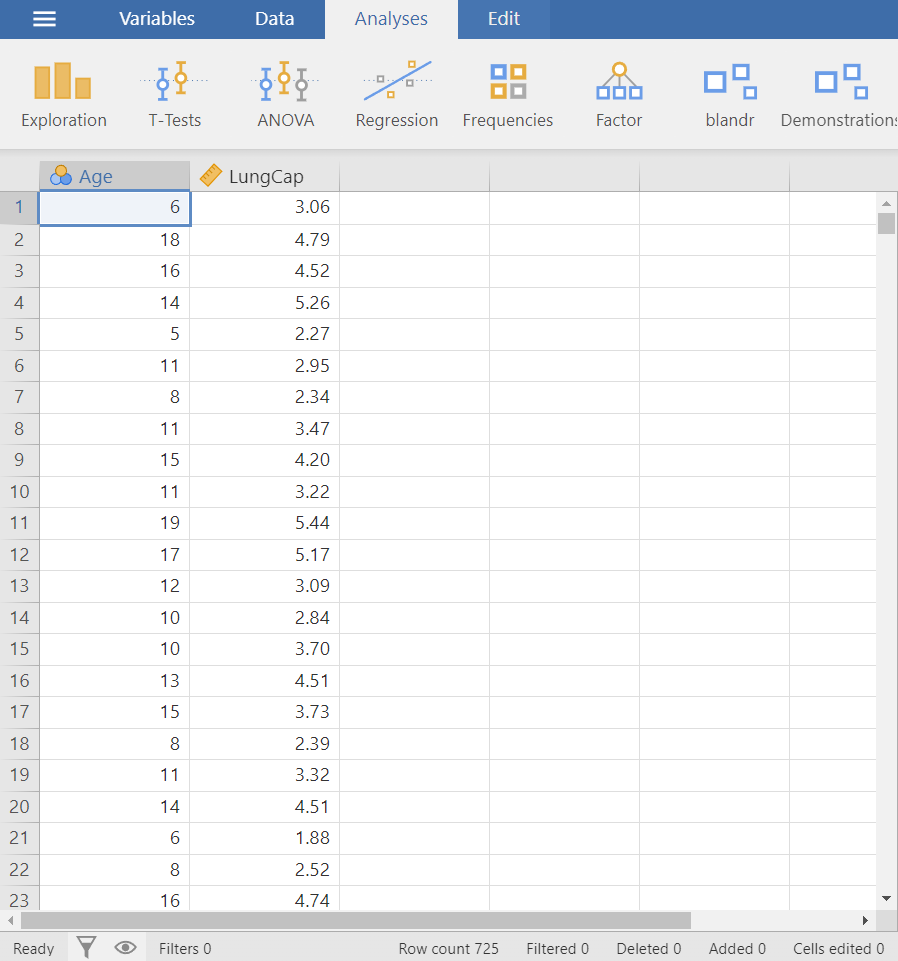
In this Lab, we will use the “LungCapacity” dataset.

8.0.1 Opening the file

Open the dataset named “LungCapacity” from the file tab in the menu:

Double-click on the variable name Age and change the measure type from nominal to continuous .

8.0.2 Research question

Let’s say that we want to model the association between age (in years) and lung capacity (in liters) for the sample of 725 participants in a survey. In other words, we want to find the parameters of a mathematical equation such as $y = α + β \cdot x$ .

8.0.3 Hypothesis Testsing

Null hypothesis and alternative hypothesis

$H_{0} :$ the two variables are not linearly related. There is no effect between age and lung capacity ( $β = 0$ ).
$H_{1} :$ the two variables are linearly related. There is an effect between age and lung capacity ( $β \neq 0$ ).

8.0.4 Scatter plot

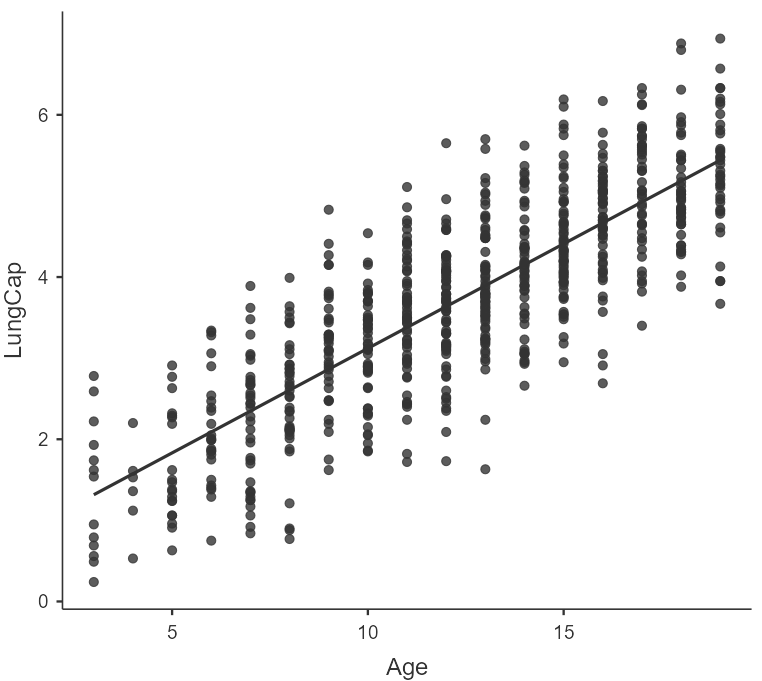
We start our analysis by creating the scatter plot of the response variable LungCap and the explanatory variable Age.

Figure 8.2: The Scatter plot of Age and Lung Capacity

There is a clear upward trend indicating that increase in Age tends to coincide with increase in LungCap. Moreover, the trend seems to be linear, so a straight line can capture the overall pattern.

8.0.5 Linear regression

The process of fitting a linear regression model to the data involves finding a straight line that can be considered as the best representation of the overall association between age and lung capacity.

To choose a line, we need to explain what we mean by the “best representation” of the data. A “best-fitting” line refers to the line that minimizes the sum of squared residuals (RSS). Therefore, we refer to the resulting model as the least-squares linear regression model and to the corresponding line as the least-squares regression line.

8.0.6 Fit a simple linear regression model

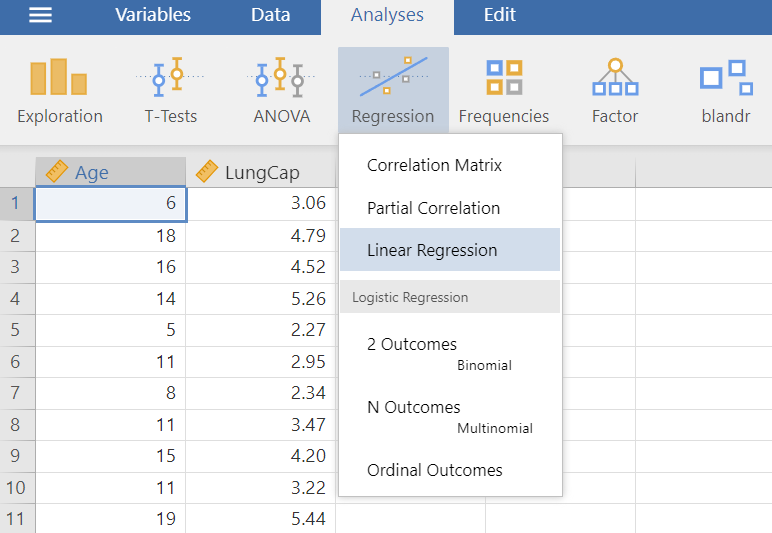
On the Jamovi top menu navigate to

as shown below (Figure 8.3).

Figure 8.3: In the menu at the top, choose Analyses > Regression > Linear Regression.

The Linear Regression dialogue box opens (Figure 8.4). From the left-hand pane drag the variable LunCap into the Dependent Variable field and the variable Age into the Covariates field on the right-hand side, as shown below:

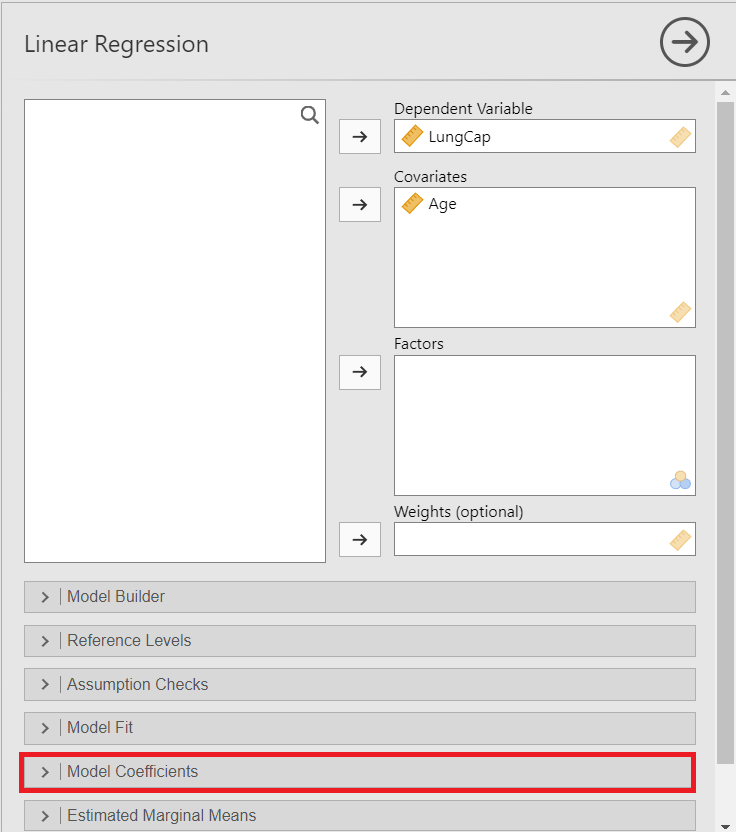
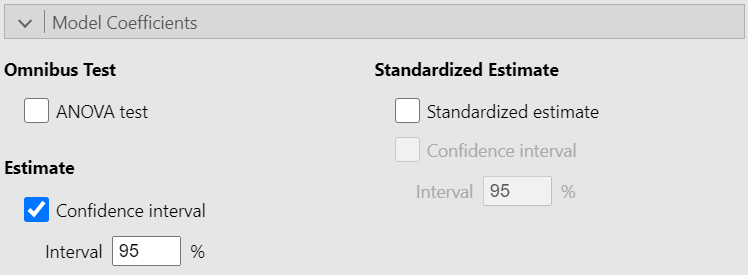
Figure 8.4: The Linear Regression dialogue box options. Drag and drop the LunCap into the Dependent Variable field and the Age into the Covariates field.

Additionally, from the Model Coefficients section tick the box “Confidence interval” in Estimate (Figure 8.5):

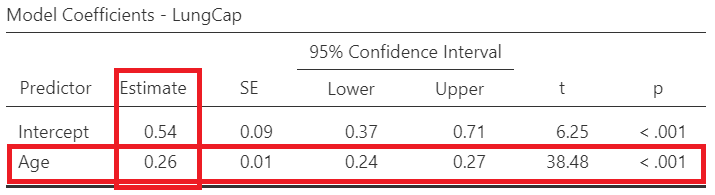
Figure 8.5: Check the Confidence interval box in the Model Coefficients section.

The output table with the model coefficients should look like the following (Figure 8.6):

Figure 8.6: The model coefficients table.

Now, let’s find the model equation from the regression table in Figure 8.6. In the Estimate column are the intercept $a = 0.54$ and the slope $b = 0.26$ for Age. Thus, the equation of the regression line becomes:

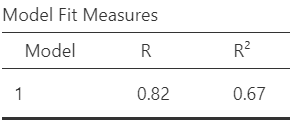
$\begin{aligned} \hat{y} & = a + b \cdot x \\ \hat{LungCap} & = a + b \cdot Age \\ \hat{LungCap} & = 0.54 + 0.26 \cdot Age \end{aligned}$

Finally, the quality of our simple linear model is presented in Figure 8.7:

Figure 8.7: The coefficient of determination $R^{2}$ .

In our example takes the value 0.67. It indicates that about 67% of the variation in lung capacity can be explained by the variation of the age. In simple linear regression $\sqrt{0.67} = 0.82$ which equals to the Pearson’s correlation coefficient, r.

Interpretation of the results

The regression coefficient (b=0.26) of the Age is significantly different from zero (p < 0.001) and indicates that there’s on average an increase of 0.26 liters in lung capacity for every 1 year increase in age. Note that the $95 %$ CI (0.24 to 0.27) does not include the hypothesized null value of zero for the slope.