8 LAB X: Simple linear regression
When we have finished this Lab, we should be able to:
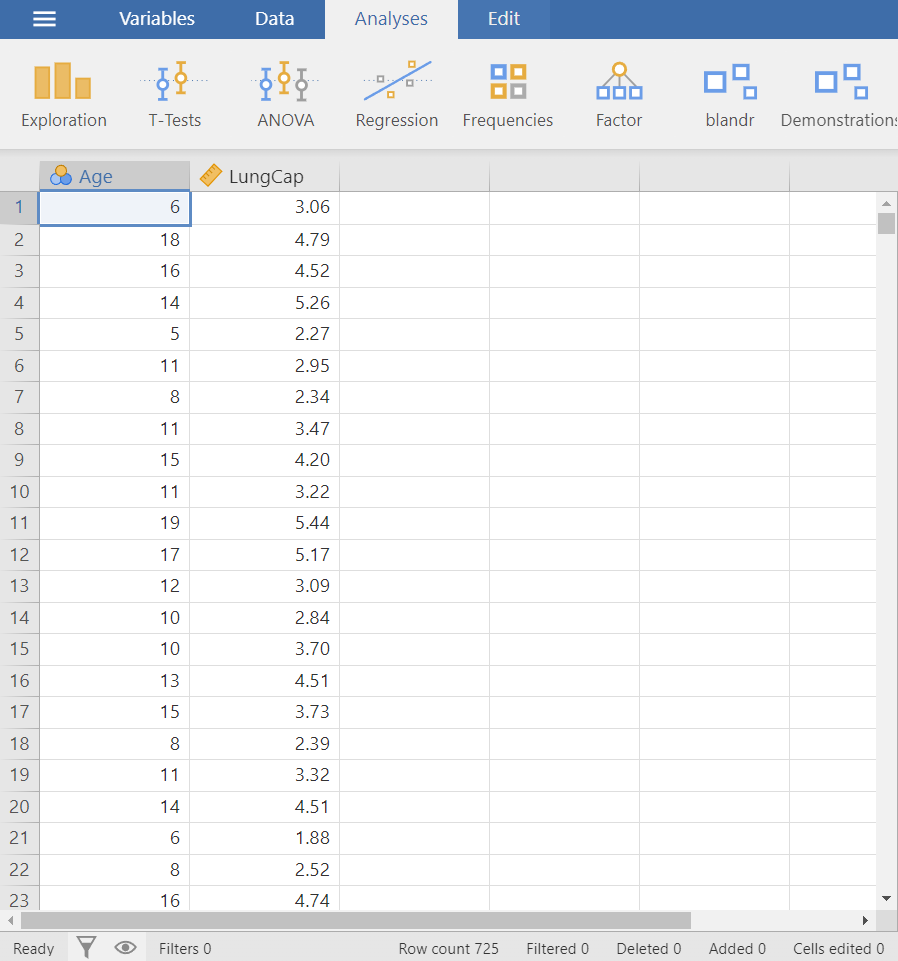
In this Lab, we will use the “LungCapacity” dataset.
8.0.1 Opening the file
Open the dataset named “LungCapacity” from the file tab in the menu:
Double-click on the variable name Age and change the measure type from nominal ![]() to continuous
to continuous ![]() .
.
8.0.2 Research question
Let’s say that we want to model the association between age (in years) and lung capacity (in liters) for the sample of 725 participants in a survey. In other words, we want to find the parameters of a mathematical equation such as
8.0.3 Hypothesis Testsing
8.0.4 Scatter plot
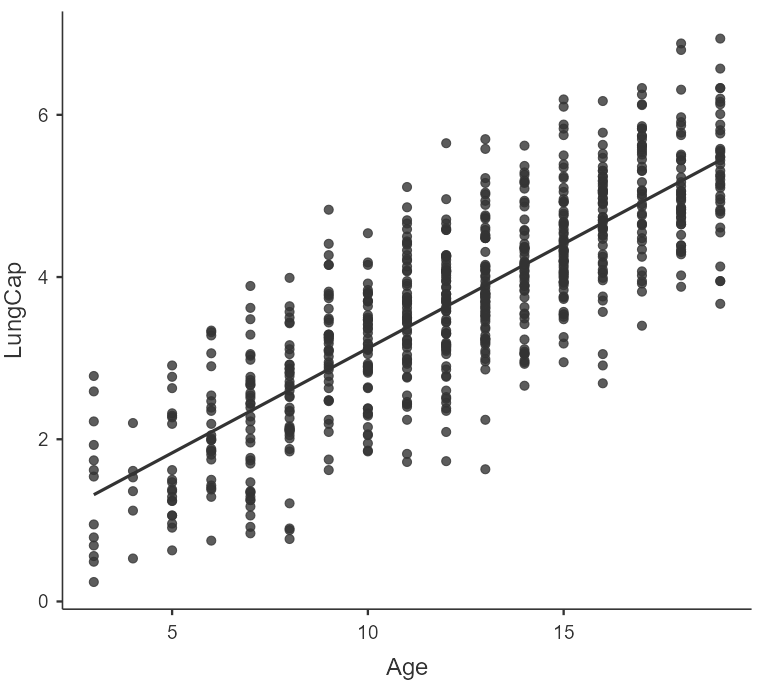
We start our analysis by creating the scatter plot of the response variable LungCap and the explanatory variable Age.
There is a clear upward trend indicating that increase in Age tends to coincide with increase in LungCap. Moreover, the trend seems to be linear, so a straight line can capture the overall pattern.
8.0.5 Linear regression
The process of fitting a linear regression model to the data involves finding a straight line that can be considered as the best representation of the overall association between age and lung capacity.
To choose a line, we need to explain what we mean by the “best representation” of the data. A “best-fitting” line refers to the line that minimizes the sum of squared residuals (RSS). Therefore, we refer to the resulting model as the least-squares linear regression model and to the corresponding line as the least-squares regression line.
8.0.6 Fit a simple linear regression model
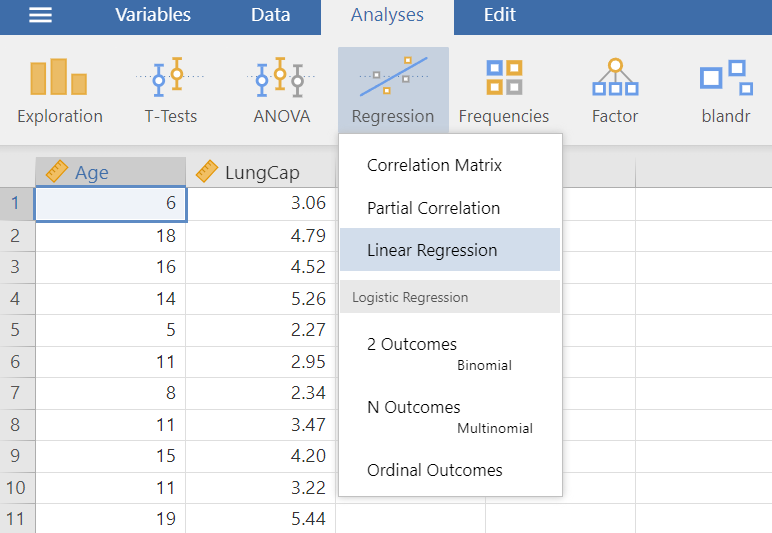
On the Jamovi top menu navigate to
as shown below (Figure 8.3).
The Linear Regression dialogue box opens (Figure 8.4). From the left-hand pane drag the variable LunCap into the Dependent Variable field and the variable Age into the Covariates field on the right-hand side, as shown below:
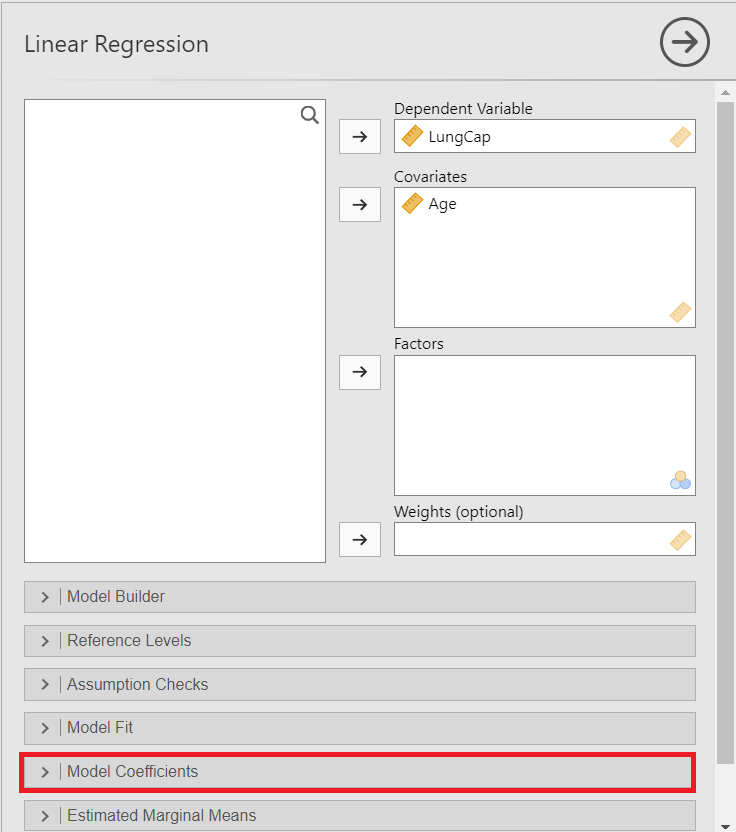
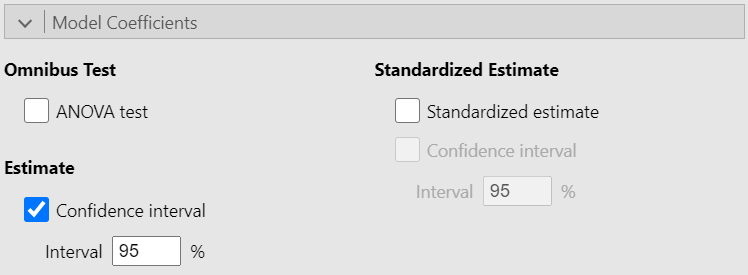
Additionally, from the Model Coefficients section tick the box “Confidence interval” in Estimate (Figure 8.5):
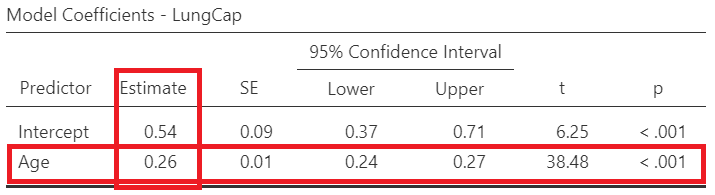
The output table with the model coefficients should look like the following (Figure 8.6):
Now, let’s find the model equation from the regression table in Figure 8.6. In the Estimate column are the intercept Age. Thus, the equation of the regression line becomes:
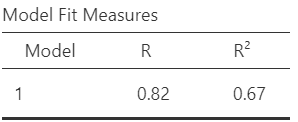
Finally, the quality of our simple linear model is presented in Figure 8.7:
In our example takes the value 0.67. It indicates that about 67% of the variation in lung capacity can be explained by the variation of the age. In simple linear regression